|
|||||||||||||||||||
|
|
|||||||||||||||||||
|
|
HUT Data Products
Navigation Links Within This Page
Time-Tagged Photon Lists (IDF.FITS Files)
Each HUT observation produces a time-tagged, photon list file, which records the X coordinate and arrival times of every photon within the observation, along with a variety of calibration information within its header. The naming format of these files is given by:
| "HUT1" or "HUT2". | Data from the Astro-1 or Astro-2 mission, respectively. |
| A 3-digit, zero-padded integer. | Designates the sequence number. |
| A 2-digit, zero-padded integer. | Designates the exposure number. |
| "idf.fits" | Specifies this is a photon-list file. |
For example, the file "HUT132701idf.fits" can be interpreted as follows. The observation occurred during the Astro-1 mission, since it begins with the sequence "HUT1" (as opposed to "HUT2"). The sequence number is "327", while the final "01" specifies that this was the first exposure within this sequence.
The format of the idf.fits files consist of a primary HDU (HDU1) and four additional HDU extensions in the form of binary tables (HDU2, HDU3, HDU4, and HDU5). The contents of these HDU's are summarized in the table below.
| TIME | float | Photon arrival time relative to EXPSTART (seconds) |
| XRAW | short | Detector X coordinate (0-2048) |
| X | short | Corrected X coordinate |
| COUNTS | long | Raw counts per pixel |
| STATUS_FLAGS | byte | Photon status flags |
| FLATFIELD | double | Flat-field correction (unitless) |
| WAVELENGTH | double | Wavelength (Å) |
| INV_SENS | double | Inverse sensitivity curve (erg/cm2/Å) |
| DT_COR_FAC | double | Dead-time correction (unitless) |
| DT_COR_ERR | double | Dead-time uncertainty (unitless) |
| TIME | float | Taken from raw file header, relative to EXPSTART (seconds) |
| STATUS_FLAGS | byte | Photon status flags |
| LIMBANG | float | Limb angle (degrees) |
| LONGITUDE | float | Spacecraft longitude (degrees) |
| LATITUDE | float | Spacecraft latitude (degrees) |
| HUT_PITCH_ERR | float | Pitch error based on HUT guide stars (degrees) |
| HUT_YAW_ERR | float | Yaw error based on HUT guide stars (degrees) |
| SOURCE_RATE | short | Excluding airglow lines (counts/second) |
| LY_ALPHA_RATE | short | Lyman α (counts/second) |
| O_I_RATE | short | O I λ1304 airglow (counts/second) |
| RATE_850_895 | short | Background rate from 850-895 Å (counts/second) |
| TIME | float | Taken from raw file header, relative to EXPSTART (seconds) |
| PIXEL_SHIFT | short | Correction for pointing error (pixels) |
| IMCS_PITCH_ERR | float | Computed pitch error (arcsec) |
| IMCS_YAW_ERR | float | Computed yaw error (arcsec) |
Extracted Spectra (CAL.FITS Files)
Each observation also has an extracted, calibrated spectrum derived from the time-tagged photon list (idf.fits file). Each extracted spectrum (cal.fits file) contains two FITS extensions. The naming convention of the file is identical to the idf.fits files. The first extension stores the extracted spectrum derived from all photons during the exposure (day + night). The second extension stores the extracted spectrum derived from just the orbital-night observations. If the entire exposure occurred during orbital night, then the extracted spectra in the first and second extensions are exactly the same. If the entire exposure occurred during orbital day, then the extracted spectrum in the second extension will have fluxes all set to zero.
The format of the cal.fits files consist of a primary HDU (HDU1) and two additional HDU extensions in the form of binary tables (HDU2 and HDU3). The contents of these HDU's are summarized in the table below.
| WAVE | float | Wavelength (Å) |
| FLUX | float | Flux (erg/cm2/s/Å) |
| ERROR | float | Poisson error in flux (erg/cm2/s/Å) |
| COUNTS | int | Raw counts, corrected for motion |
| WEIGHTS | float | Fully-corrected counts |
| WAVE | float | Wavelength (Å) |
| FLUX | float | Flux (erg/cm2/s/Å) |
| ERROR | float | Poisson error in flux (erg/cm2/s/Å) |
| COUNTS | int | Raw counts, corrected for motion |
| WEIGHTS | float | Fully-corrected counts |
TV Guider Images (TV.FITS Files)
Each observation can also contain one or more images of the target field (tv.fits files). The format of the tv.fits files consist of a single HDU, which contains the file header keywords from the associated idf.fits file, as well as a complete set of astrometric keywords.
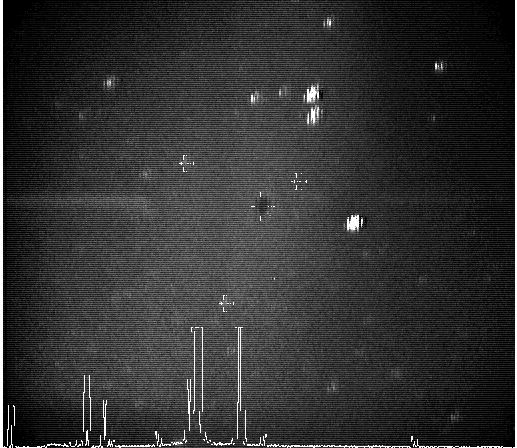
A sample guider image for NGC 6791 is displayed below. The primary target is centered in the middle of the image on the cross hair. Guide stars are denoted by crosses, while the current, cumulative histogram of the spectrum is shown below. These images will allow users to confirm the location and orientation of the aperture relative to the primary target and guide stars.
Quick-Look (Preview) Postscript Plots
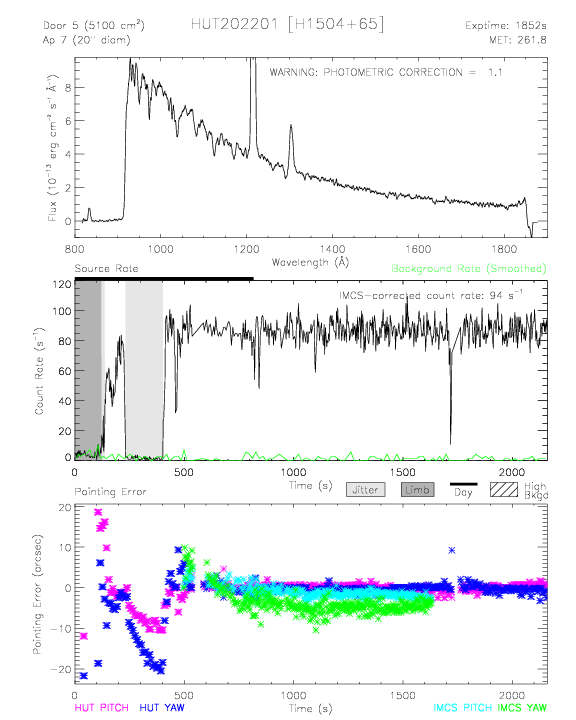
Each observation has a quick-look plot made of the extracted spectrum, consisting of three panels. The top panel plots the extracted flux as a function of wavelength. The middle panel plots the count rate of the source per second as a function of time. Areas where the target was less than 15 degrees from the Earth's limb, fell out of the aperture, occurred during orbital day time, experienced large amounts of pointing jitter, or passed through the South Atlantic Anomaly (SAA) are marked on this plot. The bottom panel plots the pitch and yaw errors computed from the guide stars and IMCS as different colored points. Additional information printed on the plots include the aperture used, total exposure time, and the IMCS-corrected count rates (if present).
These plots are available through the "Preview" pages, which can be found by clicking on the links in the "Data ID" column in the Search Results page after conducting a search through the HUT Search Form. They are also bundled with the associated idf.fits, cal.fits, and tv.fits files for download. An example quick-look plot for the white dwarf H1504+65 is shown below.
Photon Status Flag Bit Codes
Below is a summary of the values for each bit code in the photon status flags.
| 8 | User-defined bad-time interval |
| 7 | Not used |
| 6 | Target out of aperture |
| 5 | Background unacceptably high |
| 4 | Observations during SAA (Astro-1 mission only) |
| 3 | Limb-angle violation |
| 2 | Airglow feature |
| 1 | Day/Night flag (day=1, night=0) |
|
|
|




 Follow Us
Follow Us