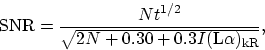Next: Conversions to Fly on
Up: High Resolution Spectroscopy in
Previous: Signal Processing and Storage
The combined efficiency of the IMAPS optical system and the detector
lead to a nominal effective area of about 4.5cm2 for
wavelengths longward of about 1000Å.![[*]](http://www.stsci.edu/icons//foot_motif.gif) For shorter wavelengths, the drop in
efficiency follows the square of the relative decrease in the
reflectivity of Al with a LiF overcoat (Lowrance & Carruthers 1981).
For shorter wavelengths, the drop in
efficiency follows the square of the relative decrease in the
reflectivity of Al with a LiF overcoat (Lowrance & Carruthers 1981).
To calculate the sensitivity of IMAPS in practical astronomical
applications, one must factor in several sources of noise that add to
the Poisson statistical fluctuations in the number of detected photons:
- 1.
- Scattered light from the gratings, principally from the echelle.
- 2.
- Readout and dark-current noise from the CCD.
- 3.
- The geocoronal Lyman-
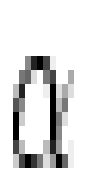 background, some of which can pass
through the mechanical collimator (§3.1).
background, some of which can pass
through the mechanical collimator (§3.1).
Items (1) and (3) above are additional sources of uv light whose
statistical fluctuations add to those of the desired spectral signal.
For the purposes of estimating a net signal-to-noise ratio, these
illuminations can be thought of as being perfectly uniform. Item (2) is
a noise signal whose amplitude is independent of the uv illumination.
As a simplification to a more elaborate procedure discussed in
§7.10, we may think of a spectrum being extracted by a slit
that is 1 CCD pixel wide and 4 pixels tall, which covers the vertical
extent of most of the intensity within an order widened by astigmatism
from the echelle grating (§3.2). Within the
4 × 1 extraction rectangle, the rms readout noise is equivalent to 0.55
photons in an integration time lasting 1 second. This is equivalent to
the statistical fluctuations in a hypothetical uniform background
illumination of 0.30 s-1 added to the spectrum's
signal. For a continuum source (i.e., a hot star), the scattered light
background is about equal to that of the spectrum itself. The diffuse
Lyman-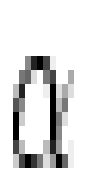 background produces about 0.3 events s-1
kR-1 in an extraction rectangle near the top of our image format
(at 1150Å), and it decreases by at the bottom (950Å)
because of the increased baffling by the mechanical collimator.
background produces about 0.3 events s-1
kR-1 in an extraction rectangle near the top of our image format
(at 1150Å), and it decreases by at the bottom (950Å)
because of the increased baffling by the mechanical collimator.
For the energy gathered over a wavelength spanned by 1 CCD pixel in the
horizontal (echelle dispersion) direction, one should expect to find the
signal-to-noise ratio given by the relation,
| 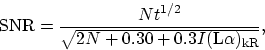 |
(1) |
where t is the integration time in seconds, N is product of the
instrument's effective area and the target's photon flux within a
wavelength interval 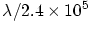 , and
, and 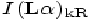 is the intensity of the geocoronal emission expressed in
kiloRayleighs. As a rough guide,
is the intensity of the geocoronal emission expressed in
kiloRayleighs. As a rough guide, 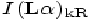 is about 2
at night and 20 on the daytime side of an orbit. However, there is a
strong dependence on solar activity and viewing geometry. Useful
guidance on typical values for the geocoronal emission are given by
Meier & Mange (1970, 1973) .
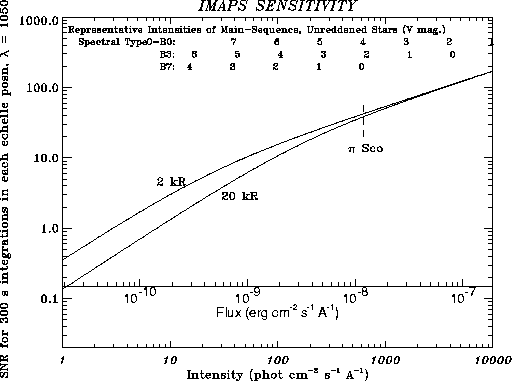
Fig. 3 shows a plot of the outcome of Eq. 1 for
an integration time of 300 seconds per echelle position. In a typical
orbit, one can expect to obtain about 1 to 3 times this amount of
on-target time for a given object in the sky. Two curves are shown: one
for
is about 2
at night and 20 on the daytime side of an orbit. However, there is a
strong dependence on solar activity and viewing geometry. Useful
guidance on typical values for the geocoronal emission are given by
Meier & Mange (1970, 1973) .
Fig. 3 shows a plot of the outcome of Eq. 1 for
an integration time of 300 seconds per echelle position. In a typical
orbit, one can expect to obtain about 1 to 3 times this amount of
on-target time for a given object in the sky. Two curves are shown: one
for 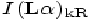 = 2 and the other for
= 2 and the other for 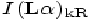 = 20. As an example, the star
= 20. As an example, the star 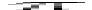 Sco has a flux
equal to 630 photons
Sco has a flux
equal to 630 photons 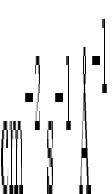 at
1050Å, and thus at this wavelength we could expect a SNR = 40. This
is about twice the SNR of the
at
1050Å, and thus at this wavelength we could expect a SNR = 40. This
is about twice the SNR of the 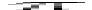 Sco spectrum that was obtained by
Jenkins, et al. (1989) on the relatively brief 5-minute observing time
of a sounding rocket flight (§2).
Sco spectrum that was obtained by
Jenkins, et al. (1989) on the relatively brief 5-minute observing time
of a sounding rocket flight (§2).
Figure: 3
Expected signal-to-noise ratios for spectra recorded by IMAPS
in 300 s, as a function of the target's continuum intensity. The two
curves show the outcome of Eq.1 for two values of
the geocoronal Lyman- diffuse background emission, diffuse background emission, 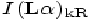 . Numbers at the top of the plot show the
approximate fluxes of stars of various spectral types and V
magnitudes. . Numbers at the top of the plot show the
approximate fluxes of stars of various spectral types and V
magnitudes. |
 |



Next: Conversions to Fly on
Up: High Resolution Spectroscopy in
Previous: Signal Processing and Storage
12/15/1998
![]() background produces about 0.3 events s-1
kR-1 in an extraction rectangle near the top of our image format
(at 1150Å), and it decreases by at the bottom (950Å)
because of the increased baffling by the mechanical collimator.
background produces about 0.3 events s-1
kR-1 in an extraction rectangle near the top of our image format
(at 1150Å), and it decreases by at the bottom (950Å)
because of the increased baffling by the mechanical collimator.