


Next: 11.2.2 Absolute Flux Calibration
Up: 11.2 High-Dispersion Absolute Flux
Previous: 11.2 High-Dispersion Absolute Flux
A distinctive feature of echelle gratings is the variation in
sensitivity as a function of wavelength within a spectral order,
commonly known as the blaze function. The adjustment applied to
eliminate this characteristic is referred to as a ripple correction. The
use of the term ``ripple'' becomes apparent when the net fluxes in
successive orders are plotted as a function of wavelength. A series of
scalloped or ripple patterns appear which must be corrected for prior to
the application of the absolute calibration.
The ripple correction and all associated equations are defined in
Cassatella (1996, 1997a, 1997b). The basic form of the ripple correction
as a function of order number and wavelength is:
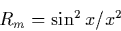
where x is expressed as:
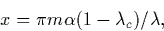
the 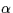 parameter is given as a function of order number:
parameter is given as a function of order number:
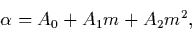
and the central wavelength corresponding to the peak of the blaze is:
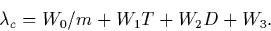
Note that unlike the SWP camera, the LWP and LWR ripple corrections do
not exhibit a dependence of central wavelength on THDA; instead the
observed central wavelengths vary linearly with time. In addition, the
LWR 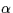 parameter evinces a bimodal behavior which has been fit
with two separate functions (i.e., a linear and a quadratic polynomial).
Here, m is order number,
parameter evinces a bimodal behavior which has been fit
with two separate functions (i.e., a linear and a quadratic polynomial).
Here, m is order number, 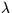 is wavelength in Ångstroms, T
is the THDA, and D is the observation date in decimal years. The
ripple correction is applied to the net flux prior to the application of
the heliocentric velocity correction to the wavelengths. The various
ripple coefficients used in the above equations are given in
Table 11.10 for each camera.
is wavelength in Ångstroms, T
is the THDA, and D is the observation date in decimal years. The
ripple correction is applied to the net flux prior to the application of
the heliocentric velocity correction to the wavelengths. The various
ripple coefficients used in the above equations are given in
Table 11.10 for each camera.
Table 11.10:
High-Dispersion Ripple Coefficients
| Coefficients |
LWP |
LWR |
SWP |
| |
|
m < 101 |
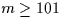 |
|
| A0 |
0.406835 |
3.757863 |
1.360633 |
0.926208 |
| A1 |
0.01077191 |
-0.0640201 |
-4.252626e-3 |
0.0007890132 |
| A2 |
-5.945406e-5 |
3.5664390e-4 |
0.0 |
0.0 |
| |
| W0 |
230868.177 |
230538.518 |
137508.316 |
| W1 |
0.0 |
0.0 |
0.0321729 |
| W2 |
-0.0263910 |
-0.0425003 |
0.0 |
| W3 |
56.433405 |
90.768579 |
2.111841 |
|



Next: 11.2.2 Absolute Flux Calibration
Up: 11.2 High-Dispersion Absolute Flux
Previous: 11.2 High-Dispersion Absolute Flux
Karen Levay
12/4/1997
![]()
![]()
![]()
![]()