


Next: Some Practical Considerations
Up: Optimal Extraction
Previous: General Principles
At a given 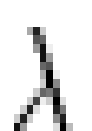 on order m, there is a true signal level
equivalent to
on order m, there is a true signal level
equivalent to  photons accumulated over n exposures
that were added together. This signal is spread over a vertical extent
of approximately 20 pixels. The actual signal sensed in each pixel is
quantized and has the usual Poisson statistical fluctuations. On
average (in the absence of statistical uncertainties) the expected
numerical outcome in each pixel identified by a subscript i is
photons accumulated over n exposures
that were added together. This signal is spread over a vertical extent
of approximately 20 pixels. The actual signal sensed in each pixel is
quantized and has the usual Poisson statistical fluctuations. On
average (in the absence of statistical uncertainties) the expected
numerical outcome in each pixel identified by a subscript i is
|  |
(6) |
where
- i
- is the index that describes the y location of a pixel or
horizontal slice, with i=0 being set at the location of maximum
intensity for order m.
- bi
- is the fraction of energy deposited in a particular
horizontal section i of an order (normalized such that
 ).
).

- is the sensitivity pattern's attenuation function
averaged over n images. It is normalized so that an interblob region
has
 , and thus
, and thus  would be the signal
registered if there were no blobs with reduced sensitivity.
would be the signal
registered if there were no blobs with reduced sensitivity.
- r
- is the background illumination level.
Figure 12:
An illustration of how to determine the most likely spectrum
intensity 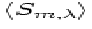 along an order m at
wavelength along an order m at
wavelength 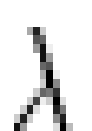 . The height of the surface above the horizontal
x-i plane represents the recorded image intensity. Small squares show
measurements of . The height of the surface above the horizontal
x-i plane represents the recorded image intensity. Small squares show
measurements of  from i=-5 to +5. The from i=-5 to +5. The  's show
the samples taken to determine the most likely intensities 's show
the samples taken to determine the most likely intensities  and and  of the
contaminating orders. The entire pattern is elevated above a general
background r, and the holes represent depressions in the sensitivity of the
contaminating orders. The entire pattern is elevated above a general
background r, and the holes represent depressions in the sensitivity
 . .
|
 |
The  and
and  terms are signals in the
adjacent orders that can contaminate our sampling of
terms are signals in the
adjacent orders that can contaminate our sampling of  .
They must be evaluated and subtracted out, and because of their
uncertainties, they lower the reliability of outlying samples of
.
They must be evaluated and subtracted out, and because of their
uncertainties, they lower the reliability of outlying samples of
 -- an effect that must be recognized when the relative
weights are assigned for different i. To estimate these contamination
contributions, we sampled the adjacent orders at positions near their
cores, but slightly offset in the direction of the order m (see
Fig. 12). This offset insures, to first order, that small
errors in centering on order m automatically adjust the contamination
correction in the right direction.
-- an effect that must be recognized when the relative
weights are assigned for different i. To estimate these contamination
contributions, we sampled the adjacent orders at positions near their
cores, but slightly offset in the direction of the order m (see
Fig. 12). This offset insures, to first order, that small
errors in centering on order m automatically adjust the contamination
correction in the right direction.
In setting up formulae for the variances of quantities that would come
from hypothetical, repeated trials of the experiment, we must express
the outcome using a general value for S, called Sm as
distinguished from  , because we do not want the weight
factors to be influenced by the local chance fluctuations on top of the
desired and contamination signals. In practice, Sm can be pictured
in terms of an average of
, because we do not want the weight
factors to be influenced by the local chance fluctuations on top of the
desired and contamination signals. In practice, Sm can be pictured
in terms of an average of  over a range of
over a range of 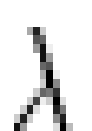 that
is large enough to make such fluctuations inconsequential.
that
is large enough to make such fluctuations inconsequential.
Imagine that we could perform repeated trial measurements of Ii. We
should expect to find a variance,
|  |
(7) |
where  is the rms readout plus CCD dark current noise
(§
is the rms readout plus CCD dark current noise
(§![[*]](http://www.stsci.edu/icons//cross_ref_motif.gif) ) (expressed as an amplitude relative to that of a
single photoevent). Numerically,
) (expressed as an amplitude relative to that of a
single photoevent). Numerically,  for a 511-frame
integration over 34 s.
The most effective approach for reconstructing S is to evaluate at all
for a 511-frame
integration over 34 s.
The most effective approach for reconstructing S is to evaluate at all
 the individual estimates for the most probable values for
the individual estimates for the most probable values for
 , which we designate as
, which we designate as 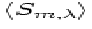 :
:
|  |
(8) |
In the numerator, the first term is the basic measurement that has
random fluctuations governed by Eq. 7. The second term is an
ultraviolet background correction term that does not vary (i.e.,
it is a global correction, except for a general trend that follows the
blaze function of the echelle grating). The third and fourth terms are
correction factors that must be applied to cancel out the contamination
signals from adjacent orders. These two terms have variations of their
own that corrupt the correction process, since we can not measure
 and
and  with perfect accuracy. The
magnitude of these corrections depend on exactly how we sample the
adjacent orders (preferably, near enough to their centers that we do not
have to worry about these orders being contaminated!)
with perfect accuracy. The
magnitude of these corrections depend on exactly how we sample the
adjacent orders (preferably, near enough to their centers that we do not
have to worry about these orders being contaminated!)
Associated with 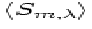 is its variance,
is its variance,
where  and
and  are determined through Eq. 7 without the
correction terms because of the deliberate, very limited sampling
reasonably near these orders' centers (to avoid the complexity of second
order contamination corrections upon the first order ones).
are determined through Eq. 7 without the
correction terms because of the deliberate, very limited sampling
reasonably near these orders' centers (to avoid the complexity of second
order contamination corrections upon the first order ones).
Specifically, the intensities of the adjacent orders are determined by
two measurements in each case, such that
|  |
(9) |
and
|  |
(10) |
The choice of using i = 7 and 8 is a matter of judgement.
Measurements closer to the centers of the other orders will be more
accurate. However, we then lose the automatic compensation for
centering errors. The simple sum without weight factors reduces the
complexity of the equation and is justified on the basis that b2 is
not very different from b3. As before, the expected variance in the
estimate is given by
|  |
(11) |
and likewise for  .
.
Now that we have derived formulae for the best estimate of
 and its reliability for a given value of i, we must
combine the measurements at different i in an optimum manner. We also
need to have a measure of the uncertainty in the outcome, in case we
wish to combine the extraction with other ones.
and its reliability for a given value of i, we must
combine the measurements at different i in an optimum manner. We also
need to have a measure of the uncertainty in the outcome, in case we
wish to combine the extraction with other ones.
For measurements with different uncertainties, the standard way to
combine them is by evaluating a weighted average, with weights that are
inversely proportional to the variances:
| ![\begin{displaymath}
\langle S_{m,\lambda}\rangle = {\sum_i\bigl[\langle
S_{m,\la...
...i\bigl[ 1 /{\rm Var} (\langle S_{m,\lambda}\rangle
)_i\bigr]}~.\end{displaymath}](img88.gif) |
(12) |
The error in the result is given by
| ![\begin{displaymath}
\sigma(\langle S_{m,\lambda}\rangle) = \Bigl\{ \sum_i\,\bigl...
...{\rm
Var} (\langle S_{m,\lambda}\rangle )_i\bigr]\Bigr\}^{-1/2}\end{displaymath}](img89.gif) |
(13) |
The combination shown in Eq. 13 is not strictly ideal,
because the correction terms for interference from adjacent orders will
have correlated errors. This effect is probably rather small, since
errors are strongly dominated by the background fluctuations (in the r
terms) in cases where the correction amounts to much.



Next: Some Practical Considerations
Up: Optimal Extraction
Previous: General Principles
Karen Levay
12/15/1998
![]() , because we do not want the weight
factors to be influenced by the local chance fluctuations on top of the
desired and contamination signals. In practice, Sm can be pictured
in terms of an average of
, because we do not want the weight
factors to be influenced by the local chance fluctuations on top of the
desired and contamination signals. In practice, Sm can be pictured
in terms of an average of ![]() over a range of
over a range of ![]() that
is large enough to make such fluctuations inconsequential.
that
is large enough to make such fluctuations inconsequential.
![]() is its variance,
is its variance,
![]() and its reliability for a given value of i, we must
combine the measurements at different i in an optimum manner. We also
need to have a measure of the uncertainty in the outcome, in case we
wish to combine the extraction with other ones.
and its reliability for a given value of i, we must
combine the measurements at different i in an optimum manner. We also
need to have a measure of the uncertainty in the outcome, in case we
wish to combine the extraction with other ones.