


Next: 11.2 High-Dispersion Absolute Flux
Up: 11.1 Low-Dispersion Absolute Flux
Previous: 11.1.5 Temperature-Dependent Degradation Correction
It is important to note that, as implemented in the image processing
software, the interpolated inverse sensitivity values, time- and
temperature-dependent sensitivity corrections, effective exposure time
normalization, and any overall gain correction factor (for non-standard
exposure or read gain or LWR UVC voltage settings) are computed as
independent correction factors and then all applied simultaneously to
the net flux and sigma spectra to result in fully calibrated and
corrected spectra in absolute flux units. The net flux spectrum (in FN
units), as determined by SWET, that is retained in the
low-dispersion extracted spectrum does not have any of these correction
factors applied to it. The calibrations and corrections are applied as
follows:
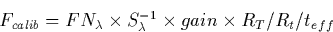
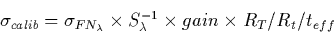
where 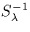 is the inverse sensitivity (including any
necessary S/L or T/L response corrections), gain is the cumulative UVC
voltage and gain correction factor (if necessary), Rt and
RT are the time- and temperature-dependent sensitivity
correction factors, respectively, and teff is the effective
exposure time. The values for
is the inverse sensitivity (including any
necessary S/L or T/L response corrections), gain is the cumulative UVC
voltage and gain correction factor (if necessary), Rt and
RT are the time- and temperature-dependent sensitivity
correction factors, respectively, and teff is the effective
exposure time. The values for 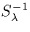 and Rt are
evaluated at the wavelength of each pixel through quadratic and nearest
neighbor interpolation, respectively, of their tabulated values. The
resulting absolutely calibrated units are ergs/cm2/Å/sec.
and Rt are
evaluated at the wavelength of each pixel through quadratic and nearest
neighbor interpolation, respectively, of their tabulated values. The
resulting absolutely calibrated units are ergs/cm2/Å/sec.



Next: 11.2 High-Dispersion Absolute Flux
Up: 11.1 Low-Dispersion Absolute Flux
Previous: 11.1.5 Temperature-Dependent Degradation Correction
Karen Levay
12/4/1997
![]()
![]()