


Next: 11.1.2 Aperture Response Corrections
Up: 11.1 Low-Dispersion Absolute Flux
Previous: 11.1 Low-Dispersion Absolute Flux
Absolute flux calibrations have been derived for the low-dispersion
modes of the IUE cameras through observations of ultraviolet
photometric standard stars, as well as observations and models of the
white dwarf star, G191-B2B. The wavelength-dependence of the inverse
sensitivity function (S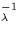 ) for each camera has been
determined by comparison of IUE observations of the white dwarf star
with model atmosphere calculations that were provided to the IUE
project by D. Finley. The overall zeropoint of the calibration curves
has been set by applying the white dwarf derived
S
) for each camera has been
determined by comparison of IUE observations of the white dwarf star
with model atmosphere calculations that were provided to the IUE
project by D. Finley. The overall zeropoint of the calibration curves
has been set by applying the white dwarf derived
S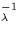 values to IUE observations of ultraviolet photometric standard stars
and comparing these results with OAO-2 measurements in the
2100-2300Å band (see González-Riestra, Cassatella, and de la
Fuente 1992 for details regarding the calibration procedures).
values to IUE observations of ultraviolet photometric standard stars
and comparing these results with OAO-2 measurements in the
2100-2300Å band (see González-Riestra, Cassatella, and de la
Fuente 1992 for details regarding the calibration procedures).
The final S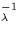 curves for the LWP, LWR (ITFs A and B), and
SWP, defined in 15Å bins for the long-wavelength cameras and 10Å bins for the SWP and fit with spline curves, are listed in
Tables 11.1-11.4. The absolute flux at a given
wavelength, F
curves for the LWP, LWR (ITFs A and B), and
SWP, defined in 15Å bins for the long-wavelength cameras and 10Å bins for the SWP and fit with spline curves, are listed in
Tables 11.1-11.4. The absolute flux at a given
wavelength, F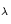 (ergs sec-1 cm-2 Å-1), is
computed as follows:
(ergs sec-1 cm-2 Å-1), is
computed as follows:
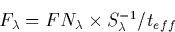
where 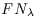 is the extracted net flux in FN units,
S
is the extracted net flux in FN units,
S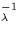 is the inverse sensitivity value at that wavelength,
and teff is the effective exposure time in seconds. The inverse
sensitivity value at a particular wavelength is determined by quadratic
interpolation of the tabulated values for a given camera.
is the inverse sensitivity value at that wavelength,
and teff is the effective exposure time in seconds. The inverse
sensitivity value at a particular wavelength is determined by quadratic
interpolation of the tabulated values for a given camera.
The effective exposure time for non-trailed (e.g., point, extended,
flat-field) sources is derived from the original commanded exposure
time, tcom, and takes into account the effects of On-Board Computer
(OBC) tick rounding and the camera rise time, trise, as follows:
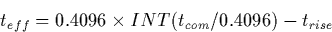
where the values of trise for each camera are taken from
González-Riestra (1991) and are 0.123, 0.126, and 0.130 for the LWP,
LWR, and SWP cameras, respectively. Tick rounding results from the
integer arithmetic used by the OBC in commanding exposures. Effective
exposure times for large-aperture trailed observations are determined
according to:
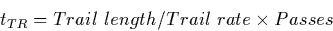
where Trail length is the trail path length of the aperture in arcsec,
Trail rate is the effective trail rate in arcsec/sec, and Passes is
the number of passes across the aperture. Because the OBC uses integer
arithmetic in calculating fixed rate slews, there is a truncation in the
commanded trail rate. This ``rounding off'' is similar to the OBC
quantitization of non-trailed exposure times. The effective trail rate
is calculated using the following equation:
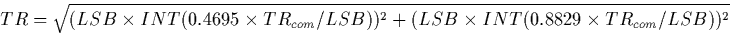
where LSB is the least significant bit (0.03001548/32 arcsec/sec) and
TRcom is the commanded trail rate.



Next: 11.1.2 Aperture Response Corrections
Up: 11.1 Low-Dispersion Absolute Flux
Previous: 11.1 Low-Dispersion Absolute Flux
Karen Levay
12/4/1997
![]() ) for each camera has been
determined by comparison of IUE observations of the white dwarf star
with model atmosphere calculations that were provided to the IUE
project by D. Finley. The overall zeropoint of the calibration curves
has been set by applying the white dwarf derived
S
) for each camera has been
determined by comparison of IUE observations of the white dwarf star
with model atmosphere calculations that were provided to the IUE
project by D. Finley. The overall zeropoint of the calibration curves
has been set by applying the white dwarf derived
S![]() values to IUE observations of ultraviolet photometric standard stars
and comparing these results with OAO-2 measurements in the
2100-2300Å band (see González-Riestra, Cassatella, and de la
Fuente 1992 for details regarding the calibration procedures).
values to IUE observations of ultraviolet photometric standard stars
and comparing these results with OAO-2 measurements in the
2100-2300Å band (see González-Riestra, Cassatella, and de la
Fuente 1992 for details regarding the calibration procedures).
![]() curves for the LWP, LWR (ITFs A and B), and
SWP, defined in 15Å bins for the long-wavelength cameras and 10Å bins for the SWP and fit with spline curves, are listed in
Tables 11.1-11.4. The absolute flux at a given
wavelength, F
curves for the LWP, LWR (ITFs A and B), and
SWP, defined in 15Å bins for the long-wavelength cameras and 10Å bins for the SWP and fit with spline curves, are listed in
Tables 11.1-11.4. The absolute flux at a given
wavelength, F![]() (ergs sec-1 cm-2 Å-1), is
computed as follows:
(ergs sec-1 cm-2 Å-1), is
computed as follows:
![]()
![]()
![]()
![]()