


High and low dispersion small-aperture spectra of the on-board hollow cathode
platinum-neon calibration lamp are used to determine wavelength as a function
of position in the image. These wavelength calibration (WAVECAL) exposures
are obtained approximately every two weeks and are usually a combination of
the calibration spectrum and a tungsten flood-lamp (TFLOOD) exposure. The
TFLOOD exposure was originally added to raise the DN level of the fainter
emission lines but is also currently used to allow reseau marks to be located
on the low dispersion WAVECAL images. These "found reseau" positions are used
to perform the geometric correction as described below.
It is important to point out that the geometric distortion characteristic of
raw IUE images (Section
4)
requires that the fitting of analytic dispersion
relations (Section
6.2)
be performed in geometrically corrected image space.
Consequently, although spectral data images are no longer explicitly
geometrically corrected in standard IUESIPS processing, WAVECAL images
are
geometrically corrected and all derived dispersion relations refer to
geometrically correct space. The G-1 geometric mapping function
Section
( 4.4.1)
is then used throughout the software system to transfer the dispersion
relations to raw-image space.
Each set of calibration images is processed to provide analytic relations
between wavelength and the line and sample position of a pixel in
geometrically correct space. Prior to 6 January 1984 the geometric correction
for WAVECAL images was applied using the reseau positions measured on a
separate TFLOOD image which was acquired close in time to the low and high
dispersion WAVECAL images. As mentioned above, the geometric correction is
now applied using reseau positions measured on the low dispersion WAVECAL
images. The applications program RSFIX is used to "fill in" reseau positions
(using bilinear interpolation of neighboring reseaux) which cannot be
accurately determined because of superimposed emission lines. Although this
procedure could in principle be also used with the high dispersion WAVECAL
reseaux, it was felt that the larger expected number of bad reseau positions
would limit any improvement in the geometric correction. (See, however,
Section
6.6
on special wavelength calibration procedures).
The pixel locations of the platinum-neon emission lines are measured on the
geometrically corrected WAVECAL images by a cross-correlation search algorithm
(see Turnrose and Perry, 1977) like that used to find reseau positions. The
starting search positions are determined from the current set of mean disper
sion constants corrected for the temperature and, in the case of LWR and SWP,
the time of acquisition of the particular WAVECAL image (see Section
6.3.1).
The measured platinum-neon line positions are then combined with laboratory
values for the wavelength and order number of each emission line and used in a
regression analysis to determine a set of dispersion constants (A and B)
relating wavelength and order number to pixel location according
to the following relations:
sample number = A1Z1 + A2Z2 + A3Z3 + ............ + A7Z7
line number = B1Z1 + B2Z2 + B3Z3 + ............ + B7Z7
where
Z
1 = 1
Z
2 = m
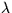
Z
3 = (m
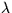
)
Z
4 = m
Z
5 =
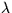
Z
6 = m
2
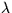
Z
7 = m
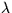 2
2
for
m = order number
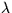 2
2
= wavelength (Å).
For low dispersion the spectral format is represented by a linear relation
(only terms 1 and 2 are used, where m = 1). For both dispersions the
analytical dispersion relations are accurate representations of the emission
line positions located using the cross-correlation search algorithm in
geometrically correct space to within one pixel (formal standard deviations of
the regression analysis are typically between 0.25 and 0.45 pixels in both the
line and the sample directions). In high dispersion, approximately 135
platinum-neon lines are typically used in the final regression; in low
dispersion between 12 and 18 lines are typically used in the final
regression. The lines available to the regression analysis form a set
referred to as a line library and are selected on the basis of the tested
ability of the automatic cross-correlation routine to find them
unambiguously. A detailed description of the high dispersion line libraries
can be found in Turnrose and Bohlin (1981). The low dispersion platinum-neon
line libraries are listed in Harvel, Turnrose, and Bohlin (1979).
The dispersion relations calculated from individual calibration images are no
longer implemented
per se in production processing.
Starting on 18 July 1980
mean dispersion constants were implemented in which approximately 25
individual dispersion relations (calculated from standard biweekly tungsten
flood-lamp and platinum-neon images obtained between 1 June 1979 and 1 June
1980) were averaged together term by term (Thompson
et al., 1980).
As more
WAVECAL images became available for analysis, updated sets of mean dispersion
constants were implemented in production processing as shown in Table
6.l. The
implementation of mean calibration data eliminated the biweekly
discontinuities in the way the IUE data were formerly reduced and also made
possible the further improvements described in Section
6.3.1 of correcting the
dispersion constants for temperature variations and secular effects.
Continual monitoring of the biweekly calibration images is conducted to
determine whether the implemented mean dispersion relations should be
modified.
Table 6-1:
History of IUESIPS Mean Dispersion Constants
| Implementation | No. of Images | End Dates | Corrections | |
|---|
| Date | Used | Start | End | Applied | Reference |
|---|
| Low Dispersion |
|---|
| LWR | 7-18-80 | 24 | 6-01-79 | 6-01-80 | none | 1 |
|---|
| | 3-03-81 | 41 | 3-31-79 | 1-01-81 | THDA & Time | 2 |
| | 9-21-82 | 46 | 1-01-80 | 8-10-82 | THDA & Time | 3 |
| | 6-20-84 | 105 | 7-15-78 | 3-07-84 | THDA & 2nd Order Time | 5 |
| |
| SWP | 7-18-80 | 24 | 6-01-79 | 6-01-80 | none | 1 |
|---|
| | 3-03-81 | 40 | 3-31-79 | 1-01-81 | THDA & Time | 2 |
| | 9-21-82 | 44 | 1-01-80 | 8-10-82 | THDA & Time | 3 |
| | 6-20-84 | 107 | 9-30-78 | 3-11-84 | THDA & 2nd Order Time | 5 |
| |
| LWP | 8-17-81 | 1 | 6-17-80 | 6-17-80 | none | |
|---|
| | 9-21-82 | 14 | 6-17-80 | 8-17-82 | none | 3 |
| | 4-12-83 | 28 | 6-17-80 | 3-21-83 | THDA | 4 |
| | 6-20-84 | 51 | 6-17-80 | 3-11-84 | THDA | 5 |
| |
| High Dispersion |
|---|
| LWR | 7-18-80 | 24 | 6-01-79 | 6-01-80 | none | 1 |
|---|
| | 4-30-81 | 41 | 3-31-79 | 1-01-81 | none | 2 |
| | 5-19-81 | 41 | 3-31-79 | 1-01-81 | THDA & Time | 2 |
| | 9-21-82 | 47 | 1-01-80 | 8-10-82 | THDA & Time | 3 |
| | 6-20-84 | 103 | 9-30-78 | 3-07-84 | THDA & 2nd Order Time | 5 |
| |
| SWP | 7-18-80 | 24 | 6-01-79 | 6-01-80 | none | 1 |
|---|
| | 4-30-81 | 41 | 3-31-79 | 1-01-81 | none | 2 |
| | 5-19-81 | 41 | 3-31-79 | 1-01-81 | THDA & Time | 2 |
| | 9-21-82 | 45 | 1-01-80 | 8-10-82 | THDA & Time | 3 |
| | 6-20-84 | 109 | 9-11-78 | 3-11-84 | THDA & 2nd Order Time | 5 |
| |
| LWP | 8-17-81 | 1 | 6-17-80 | 6-17-80 | none | - |
|---|
| | 9-21-82 | 14 | 6-17-80 | 8-17-82 | none | 3 |
| | 4-12-83 | 28 | 6-17-80 | 3-21-83 | THDA | 4 |
| | 6-20-84 | 50 | 6-17-80 | 3-11-84 | THDA | 5 |
| REFERENCES |
| 1 | Thompson, et al. (1980) |
| 2 | Thompson, Turnrose and Bohlin (1982a) |
| 3 | Thompson and Turnrose (1983) |
| 4 | Thompson (1983b) |
| 5 | Gass and Thompson (1984) |
The wavelength calibration exposures are made using the small aperture since
it provides the sharpest possible images of the calibration lamp emission
lines. The dispersion constants derived from these images define a dispersion
relation for the small aperture. When the large aperture is used to take
data, it is necessary to modify the A1 and B1 terms of the dispersion relation
to translate the dispersion line by the separation of the two apertures. The
offsets in line and sample between these apertures have been measured to an
accuracy of several tenths of a pixel unit (Turnrose et al., 1979;
Turnrose, 1983). Note that as of 1 August 1979 telescope operations and image
processing have both used the "physical center" offset values referred to in
the references above. A complete discussion of these offsets and the offsets
used earlier can be found in the listed references. The current offset values
have been given in Table
2-3 in Section
2.2.
In this section are discussed the corrections applied to the mean dispersion
relations before spectral fluxes are extracted (Section
7). These corrections
are based on the characteristics of each individual image.
Variations in spacecraft temperatures cause shifts in the location of the
spectral format with respect to the reseau grid. Additionally, it has been
found that the location of the spectral format shifts with time, apparently
independent of the temperature variations. Correlations of the systematic
behavior of these motions as a function of time and camera head amplifier
temperature (THDA) were first found for the LWR and SWP camera as are
described in Thompson, Turnrose, and Bohlin (1982a). For the LWP camera,
correlations with THDA have been determined, while correlations with time are
still being evaluated (see Thompson, 1983b).
Corrections for thermal and temporal shifts based on the derived correlations
were first implemented as part of the standard LWR and SWP data processing at
GSFC on 3 March 1981 in low dispersion and on 19 May 1981 in high dispersion
by a new IUESIPS applications program, TCCAL. Corrections for thermal (but
not temporal) shifts for LWP images were implemented on 12 April 1983.
The corrections are based on the THDA temperature at the end of the exposure
(denoted by T in the equation below, and expressed in centigrade degrees), and
the time (t) expressed as the total number of elapsed days since 1 January
1978. Both values are generally obtained from data extracted from the image
header label. The THDA at the end of exposure is normally extracted from the
camera snapshot section of the image label, but if that THDA value is not
available, then the THDA at the time of image read is extracted. If neither
THDA is available, then the processing defaults to the mean dispersion
constants unless either (a) a specific THDA value is manually specified by the
image processing specialist when the image is processed, or, (b) for LWR and
SWP images processed after 20 June 1984, a reasonable date of observation can
be extracted from the image label in which case a correction for time only is
applied. The last option above was implemented to improve the calibration of
images which do not contain valid temperature data (e.g., history playback
images and images obtained prior to about March 1979). See Section
9.3 for
information about how these data are documented in the image processing
history label.
The correction terms Ws and Wl representing a uniform shift applied to the
mean dispersion constants are defined by the general expression
Ws = W1s + W2sT + W3st + W4st2
Wl = W1l + W2lT + W3lt + W4lt2
where W
s and W
l are the corrections to be added to the A
1 and B
1 terms of the
dispersion relation respectively. The current correlation coefficients are
shown in Table
6-2. As was shown in Table
6-1, the corrections that have been
applied to the mean dispersion constants have changed along with the updated
mean dispersion constants. The previously implemented correlation coeffi
cients can be found in the references cited; the overall corrections actually
applied in production have been documented in the image label as described in
Section
9.3.
Table 6-2:
Coefficients Defining the Dispersion Relations For the Small Aperture
| | LWP HIGH | LWR HIGH | SWP HIGH |
|---|
| A1 | 5.873462158066862E 03 | -4.568022566378104E 03 | 5.240320204548078E 02 |
| A2 | -1.722858383957817E-01 | 1.446262990785922E-01 | -1.712441225166165E-01 |
| A3 | 6.555369560052370E-07 | -5.465497800144054E-07 | 1.270371733811783E-06 |
| A4 | 1.595428893061642E 01 | 3.70636790765387E-02 | 2.400037009830254E-01 |
| A5 | 3.593457426360678E-01 | 2.752782055000451E-01 | -4.501831878764407E-01 |
| A6 | -6.872232913998719E-05 | -1.128214756800759E-07 | -1.710001924922418E-06 |
| A7 | -2.783347519836731E-06 | 1.178784019429775E-07 | -1.229343742859447E-07 |
| |
| B1 | 1.722851374444825E 03 | 1.567990956548678E 04 | -7.171777625701399E 03 |
| B2 | -1.525291559975196E-01 | -2.798031396384101E-01 | -1.180881485399540E-01 |
| B3 | 6.234107147653489E-07 | 9.128413204610836E-07 | 1.221904605794151E-06 |
| B4 | 2.195447834078006E-03 | 5.258053799093249E-02 | -6.164813394499542E-02 |
| B5 | 3.116702603413883E-01 | 2.249828862644492E-01 | 3.952920335125301E-01 |
| B6 | 5.219524333350585E-08 | 2.913198089519675E-08 | 4.665040004845884E-07 |
| B7 | -2.825129628780807E-07 | 9.398635854889812E-09 | -1.466678989324729E-07 |
| |
| CORRELATION COEFFICIENTS |
|---|
| |
| W1(S) | -7.430500388145447E-01 | 5.459306716918945E 00 | -2.977794647216797E 00 |
| W2(S) | 8.040672540664673E-02 | -2.795313000679016E-01 | 4.107570648193359E-02 |
| W3(S) | | -1.768400659784675E-03 | 2.857662504538894E-03 |
| W4(S) | | 3.070972525165416E-07 | -5.223851076152641E-07 |
| |
| W1(L) | -4.000792503356934E 00 | -8.628579139709473E 00 | -2.841607093811035E 00 |
| W2(L) | 4.322262406349182E-01 | 5.308601856231689E-01 | 2.274644970893860E-01 |
| W3(L) | | 1.599742565304041E-03 | 7.730186916887760E-04 |
| W4(L) | | -3.199881462023768E-07 | -6.993195711402223E-08 |
| |
| | LWP LOW | LWR LOW | SWP LOW |
|---|
| A1 | 1.046282942865237E 03 | -2.992355784397701E 02 | 9.833223402481985E 02 |
| A2 | -2867015866237448E-01 | 3.22840587387481E-01 | 04.665747674619282E-01 |
| A3 | | | |
| A4 | | | |
| A5 | | | |
| A6 | | | |
| A7 | | | |
| |
| B1 | -2.722748512318324E 02 | -2.647551045134080E 02 | -2.633234804632572E 02 |
| B2 | 2.465361695604904E-01 | 2.256895703788157E-01 | 3.762166817667614E-01 |
| B3 | | | |
| B4 | | | |
| B5 | | | |
| B6 | | | |
| B7 | | | |
| |
| CORRELATION COEFFICIENTS |
|---|
| |
| W1(S) | -7.578814029693604E-01 | 5.142534255981445E 00 | -3.452352523803711E 00 |
| W2(S) | 8.561676740646362E-02 | -2.351302504539490E-01 | -3.286504652351141E-03 |
| W3(S) | | -1.864231890067458E-03 | 3.721332177519798E-03 |
| W4(S) | | 1.824748778744834E-07 | -6.585678420378827E-07 |
| |
| W1(L) | -2.995339393615723E 00 | -8.595767974853516E 00 | -1.659444808959961E 00 |
| W2(L) | 3.379166126251221E-01 | 4.655143022537231E-01 | 1.674554347991943E-01 |
| W3(L) | | 2.750693820416927E-03 | 2.752062573563308E-05 |
| W4(L) | | -5.675888132827822E-07 | 8.504440529577550E-08 |
The major effect of the temperature and time corrections is to shift the
location of the spectral format in the direction approximately perpendicular
to the dispersion direction in low dispersion and approximately along the
dispersion direction in high dispersion (Thompson, Turnrose, and Bohlin,
1982a). Since only the zero-point or offset terms of the dispersion relations
are corrected, there is no change to the scale of the dispersion relations.
Accordingly, the component of the correction along the dispersion direction
corresponds very nearly to a constant velocity shift in high dispersion and a
constant wavelength shift in low dispersion.
Based on the statistical analysis of the WAVECAL images used to establish the
time and temperature dependencies, the corrections described above reduced the
average relative (i.e., intrinsic) error in high dispersion wavelength
assignments to a velocity equivalent of less than 3 km s-1.
Larger relative
errors may be expected for specific wavelengths near the tube peripheries or
affected by residual uncorrected geometric distortion (see Section
6.5) and
for images exposed during times when large variations in spacecraft
temperature exist. There is limited recent evidence that overall differential
(i.e., non-uniform) motion of the spectral format may occur, which may also
increase the expected errors. This as yet ill-understood motion has been
observed to introduce non-uniformities of up to approximately 1 pixel. In
addition, extrinsic errors caused, for example, by spacecraft pointing
limitations (target decentering due to small errors in the initial
acquisition, spacecraft roll drift during long exposures, etc.) and the
uncertainty in centroiding spectral features in extracted spectra may exist
which contribute to the absolute error in IUE wavelengths. A more detailed
discussion of overall errors is presented in Section
6.5.
The time-and/or-temperature-corrected dispersion relations, as mapped into raw
image space by the G
-1 function discussed in Section
4, are used by the
spectral extraction routines described in Section
7 not only to assign
wavelengths but also to determine the position of the extraction slit as it is
passed numerically by the computer along each spectral order of the image.
Accurate gross and background flux levels therefore require proper
registration of the dispersion relation with the actual spectral orders,
particularly in the region of the closely-spaced orders in high dispersion.
Since the corrections described in Section
6.3.1 for determining the location
of the spectral format are statistical in nature, automatic and manual
registration methods are used to modify further the dispersion constants on an
image-by-image basis to remove residual registration errors in the direction
perpendicular to the dispersion. See Section
9.3 for information regarding
documentation of registration shifts in the image label.
Several modifications have been made to the automatic registration routine
DCSHIFT, as described chronologically in Turnrose and Harvel (1982) and
Turnrose, Thompson and Gass (1984). The current version which was implemented
at GSFC on 24 November 1981 is described in detail in Thompson and Bohlin
(1982). The basic technique involves using a cross-correlation spectral-
order-finding algorithm to sample the raw image at 12 discrete locations and
to determine the line and sample offsets of the spectral format relative to
the corrected dispersion relations, perpendicular to the orders themselves.
The 12 discrete search areas are now all chosen in the same spectral order, as
shown in Table
6-3. In high dispersion the registration shifts are first
calculated in the region of the closely spaced orders (order 108) where
precise registration is most critical. If these shifts do not pass certain
built-in program constraints (described in Thompson and Bohlin, 1982), up to
three progressively lower orders are searched in the same way. With the
average of the 12 offset values, IUESIPS adjusts the A
1 and B
1 terms in the
dispersion relations, in effect tailoring the dispersion relations for the
particular target image in question. Algorithms currently exist for the
automatic registration of both high and low dispersion point-source spectra
and of low dispersion trailed spectra.
Table 6-3:
Search Area Wavelengths
| Low dispersion wavelengths (Å) |
|---|
| ong wavelength | Short wavelength |
|---|
| 2100 | 1300 |
| 2200 | 1350 |
| 2300 | 1400 |
| 2400 | 1450 |
| 2500 | 1500 |
| 2600 | 1550 |
| 2700 | 1600 |
| 2800 | 1650 |
| 2900 | 1700 |
| 3000 | 1750 |
| 3100 | 1800 |
| 3200 | 1850 |
| High dispersion wavelengths (Å) |
|---|
| Long wavelength | Short wavelength |
|---|
| m= 108 | 100 | 86 | 77 | m= 108 | 100 | 82 | 77 |
|---|
| 2132 | 2303 | 2677 | 2995 | 1270 | 1372 | 1671.5 | 1782 |
| 2133.5 | 2304.5 | 2679 | 2997 | 1271 | 1373 | 1673 | 1783.5 |
| 2135 | 2306 | 2681 | 2999 | 1272 | 1374 | 1674.5 | 1785 |
| 2136.5 | 2307.5 | 2683 | 3001 | 1273 | 1375 | 1676 | 1786.5 |
| 2138 | 2309 | 2685 | 3003 | 1274 | 1376 | 1677.5 | 1788 |
| 2139.5 | 2310.5 | 2687 | 3005 | 1275 | 1377 | 1679 | 1789.5 |
| 2141 | 2312 | 2689 | 3007 | 1276 | 1378 | 1680.5 | 1791 |
| 2142.5 | 2313.5 | 2691 | 3009 | 1277 | 1379 | 1682 | 1792.5 |
| 2144 | 2315 | 2693 | 3011 | 1278 | 1380 | 1683.5 | 1794 |
| 2145.5 | 2316.5 | 2695 | 3013 | 1279 | 1381 | 1685 | 1795.5 |
| 2147 | 2318 | 2697 | 3015 | 1280 | 1382 | 1686.5 | 1797 |
| 2148.5 | 2319.5 | 2699 | 3017 | 1281 | 1383 | 1688 | 1798.5 |
In the event that DCSHIFT fails to determine an adequate shift or if requested
by the Guest Observer for a weak spectrum, a manual registration shift will be
calculated. In this mode, the raw image is displayed on the Experiment
Display System (EDS) screen with a wavelength overlay generated using the
(time-and/or-temperature-corrected) dispersion constants. If the dispersion
lines of the overlay are observed to fall to one side of the spectrum, the
image processing specialist will manually enter a shift in the sample
direction which will cause the overlay to be superimposed on the data.
IUESIPS then converts the entered sample direction shift into line and sample
offsets which correspond to an equivalent shift perpendicular to the
dispersion. These offsets are then added to the A
1 and B
1 dispersion constant
terms as described above.
Note that the GO can greatly facilitate the processing operation by specifying
on the Observatory Record Sheet (see Section
1.4) that the manual shift
routine should be used for those images which would not be suitable for the
automatic algorithm such as weak or emission-line spectra.
The errors expected with the automatic registration of point-source spectra
are generally less than 0.1 - 0.3 pixel and are slightly larger for trailed
spectra. Because of the possibility of differential motion of the spectral
format referred to in Section
6.3.1, it is possible that even perfect
registration in order 108 could leave registration errors as large as a pixel
in the lower orders (since the differential motion error generally changes
linearly across the image). Since the lower orders in high dispersion are
farther apart and since the extraction slit is intentionally made slightly
longer than the width of the spectral orders, these registration errors should
not seriously affect the extracted spectral data. Although the errors
involved in the manual registration routine will depend upon the accuracy of
the image processing specialist and the quality of the raw spectral image,
they are probably typically less than 0.5 pixel.
It may be noted that although the dispersion relation describes the spectral
format location in geometrically correct space, the correction applied refers
to a shift measured in raw image space. Theoretically the raw image space
registration shift should be converted back to an equivalent geometrically
correct shift to compensate for any expansion, contraction, or rotation of the
image that would occur in the geometric correction process. Test results
indicate, however, that this error is in fact less than a few percent of the
calculated shift and is therefore insignificant.
Following the extraction of spectral fluxes (Section
7), two additional
corrections to the assigned wavelengths are routinely made. These corrections
are described in the following subsections in order to consolidate the
discussion of wavelength topics within Section 6.
As of 10 November 1981 at GSFC, wavelengths are routinely reduced to a
heliocentric frame of reference for all high dispersion spectra except on-
board calibration lamp exposures and images for which the target coordinates
or the time of observation are not available. An observer can determine if
the correction has been performed by examination of record 0 of the MEHI file
(see Section
8.2.2.2)
or the image header label as described in Section
9.3.
Using the time of the midpoint of observation, the velocity components of the
earth and IUE in a righthanded rectangular equatorial coordinate system (+x is
toward the vernal equinox, +z is toward the north celestial pole) are computed
using the routines described in Harvel (1980). Harvel has shown that by using
the fixed orbital elements listed in that reference, the spacecraft velocity
calculation was accurate to 0.25 km s-1
over the first 3 years of IUE
operation.
(Schiffer (1982) has indicated that an observed evolution of the IUE orbital
elements may increase the error in the spacecraft velocity calculation by
about 1 km s-1.
Most of the change is in the Z component. The operations
software now stores current IUE orbital elements in the science header; see
Figure
9-1b.)
Additional spacecraft velocity errors can result from errors in
calculating the time of the midpoint of the observation. Currently
the midpoint time is set equal to the end-of-exposure time minus half of the
total exposure time, as read from the raw-image label. Depending on the
camera procedures used, this method could cause an error in the spacecraft
velocity calculation. However, since the magnitude of the spacecraft velocity
is small compared to that of the earth's motion (4 km s-1 versus
~ 30 km s-1)
the error will in general have a small effect on the overall wavelength
correction.
The computed net radial velocity of the IUE spacecraft toward the object is
then:
V = V
x cos(
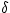
) cos(
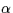
) + V
y sin(
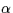
) cos(
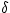
) + Vz sin(
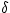
)
V
x = V
x (earth) + V
x (IUE)
V
y = V
y (earth) + V
y (IUE)
V
z = V
z (earth) + V
z (IUE)
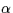
= right ascension of the object
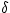
= declination of the object.
The extracted wavelengths are then corrected by:
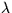 corrected
corrected = (1 + V/c)
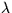 uncorrected
uncorrected
where
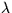 corrected
corrected
is in the heliocentric reference system and c is
the speed of light.
Note that the calculation is such that a positive net radial velocity
correction indicates a net approach of the IUE spacecraft toward the target,
following the standard convention. The individual IUE and earth velocity
components and the net radial velocity correction used are documented in the
image processing history label as discussed in Section
9.3.2.
The wavelengths obtained using the platinum-neon calibration lamp are vacuum
wavelengths. Since it is customary in the ultraviolet literature to list air
wavelengths for lines longward of 2000 Å, a vacuum-to-air wavelength
correction is applied in the processing of all images for
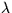
>= 2000 Å.
In the case of high dispersion spectra, this correction is made
after the heliocentric correction described in Section
6.4.1. The
formula used for wavelengths
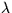 vac
vac
equal to or greater than 2000 Å is:
where
f(
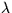
) = 1.0 + 2.735182 × 10
-4 +
131.4182/
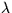 2
2 + 2.76249 × 10
8/
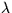 4
4
At 2000 Å, the magnitude of the correction is ~ 0.65 Å, and it increases with
wavelength to ~ 0.90 Å at 3100 Å.
Note that under the old reduction software (i.e., prior to 3 November 1980 for
low dispersion and 10 November 1981 for high dispersion) the vacuum-to-air
correction was only applied to data from the long wavelength spectrograph
(cameras LWR and LWP). It is now applied for all cameras at wavelengths
greater than or equal to 2000 Å.
The final uncertainty in the wavelength measurement of a spectral feature in
an IUE spectrum is a combination of various intrinsic and extrinsic errors.
The analysis of WAVECAL images used to establish the time and temperature
dependencies also establishes the average intrinsic error in the wavelength
calibration process.
Table 6-4
lists these average intrinsic errors for the
various time/temperature compensation methods. (Note that for SWP and LWR,
the column relevant to current production techniques is that headed "THDA &
2nd Order Time", whereas for LWP, which currently has no time dependence
applied, the relevant column is that headed "THDA Only." These errors pertain
to the limitations of modeling the behavior of dispersion relations fitted to
the rather homogeneous set of WAVECAL images. The absolute accuracy of
applying this internal wavelength scale to actual spectral images depends on a
number of other, largely extrinsic, factors. Such factors include the extent
to which the temperature and time pertinent to a given image fall within the
correlation range defined by the WAVECAL data, the extent to which spectral-
image-specific reseau motion and geometric distortion can be compensated, the
extent to which the limited-term polynomial defining the dispersion relations
can compensate for small-scale deviations from a smooth wavelength scale, the
extent to which the laboratory wavelengths assigned to the WAVECAL spectra are
correct, the extent to which the target object is centered in the aperture,
and the extent to which a feature in an extracted spectrum can be accurately
centroided. These various factors are addressed below.
Table 6-4:
Average Relative (Intrinsic) Error (1 sigma in pixels)
for Various Corrections to the Mean Dispersion Constants
| Dispersion Direction | No Correction | THDA Only | Time Only |
THDA & Time | THDA & 2nd Order Time |
|---|
| SWP High | | | | | |
| parallel | 1.07 | .81 | .41 | .26 | .24 |
| perpendicular | .49 | .49 | .23 | .18 | .15 |
| |
| SWP Low | | | | | |
| parallel | .84 | .82 | .29 | .25 | .19 |
| perpendicular | 1.03 | .86 | .36 | .30 | .28 |
| |
| LWR High | | | | | |
| parallel | 1.44 | .78 | 1.03 | .42 | .40 |
| perpendicular | .31 | .30 | .28 | .24 | .24 |
| |
| LWR Low | | | | | |
| parallel | .37 | .35 | .34 | .30 | .29 |
| perpendicular | 1.66 | 1.15 | .94 | .41 | .38 |
| |
| LWP High | | | | | |
| parallel | .64 | .38 | .63 | .38 | .36 |
| perpendicular | .35 | .19 | .34 | .18 | .18 |
| |
| LWP Low | | | | | |
| parallel | .38 | .30 | .38 | .28 | .28 |
| perpendicular | .63 | .41 | .60 | .41 | .39 |
Prior to the implementation of temperature and time corrections (reference
Table
6-1),
systematic errors were introduced for images exposed during
extreme spacecraft temperatures or at times much different than the average
time for the mean dispersion relations. Further, now that the overall time
dependence has been observed to be nonlinear (i.e., a second-order time
dependence is used), it is apparent that systematic errors were also
introduced by extrapolating the linear time correction beyond the end dates of
the input calibration data (see Table
6-1) such that the greater the
extrapolation in time, the larger the systematic error.
Because the dispersion relations, which are determined in geometrically
corrected space, are now applied to spectral images in raw image space, errors
in the mapping function G-1
represent an additional error in the assigned
wavelengths. Although studies have shown that reseau positions vary with both
temperature and image intensity (see Section
4.2,
Oliver (1979), and Thompson
1983a), IUESIPS currently uses only mean reseau positions for LWP and LWR
images and only temperature-corrected mean reseau positions for SWP images
(see Section
4.3).
The lack of any correction for image intensity can cause
errors of 1 pixel or more in the assigned reseau positions (Thompson 1984c).
Since the error occurs primarily in the line direction, it may result in a
position-dependent wavelength error corresponding to up to f 0.7 pixels. The
mean reseau positions currently used in IUESIPS are all based on an analysis
of 60-percent UVFLOOD images. Although the data set included images taken
over a fairly wide range of temperatures, they were all at approximately the
same DN level. Since the 60-percent UVFLOODs have a central mean DN
of approximately 120, the largest errors may occur for images with higher or
lower exposure levels (and at extreme spacecraft temperatures for the
uncorrected LWR and LWP cameras).
A possible source of absolute wavelength error is the inability of a
limited-term polynomial to compensate for small-scale deviations from a smooth
wavelength scale. Small-scale image distortions, when occurring in the
direction perpendicular to the dispersion, have been observed and described as
residual curvature; such distortion must certainly also occur along the
dispersion and would result in localized small-scale (sub-pixel) wavelength
errors.
Another possible explanation for errors in the assigned wavelengths, suggested
by Ayres (1984), is that errors may exist in the library of laboratory wave
lengths. In addition, Ayres suggested that the non-uniform distribution of
emission lines used in generating the dispersion relation may be such that the
fit favors the regions which contain the most emission lines. Recent work by
de La Pena (1984) shows that the SWP high dispersion wavelength assignments
show a wavelength-dependent variation of ~ 2 km s-1
which could be explained
by Ayres' suggestion. It should be noted that all the above results were
based on studies of WAVECAL images and therefore would not be subject to
reseau-position errors due to the beam-pulling effects mentioned above.
Target de-centering within the aperture can lead to appreciable absolute
wavelength errors, particularly in the large aperture, where the centering
error can typically be about an arcsecond, even larger in the case of
blind-offset acquisition. A pointing error of 1 arcsecond along the dispersion
direction is 0.66 pixel, or about 5 km s-1 in high dispersion.
As mentioned
in Section
6.3.1,
spacecraft drift during long exposures can also contribute
to de-centering error. The small size (about 3 arcseconds) of the small
aperture should result in better absolute wavelengths due to reduced target
de-centering effects.
The ability to centroid a spectral feature in an extracted spectrum is a final
limitation to the accuracy of assigned wavelengths. As is pointed out in
Thompson, Turnrose, and Bohlin (1982a), for an isolated narrow feature with
the instrumental resolution of 2.5 pixels in the cleanest IUE data, the best
possible estimate of the measurement accuracy would be a 0.25 pixel, which in
high dispersion corresponds to a 2 km s-1 velocity uncertainty.
In many
cases, the spectral data will not be of sufficient quality to approach a 0.25
pixel measurement error.
Finally, it should be remembered that the errors referred to in most of the
above discussions are AVERAGE errors, particularly those in Table
6-4. Recent
experimental results have, in general, confirmed these average errors although
it was found that the quoted averages can be misleading if used to describe
the accuracy of measuring a single spectral feature. One analysis that was
performed involved extracting several LWR and SWP high dispersion WAVECAL
spectra using standard production processing techniques and measuring the
wavelength assignment accuracy of the Pt-Ne emission lines in several orders
(Heckathorn 1984 and Thompson 1984a). It was concluded that although the
average errors found were small (i.e., the overall mean wavelength error for
each of six images was always less than 3 km s-1, larger errors were found in
measuring the wavelengths of individual lines (± 6 km s-1).
The study of reseau motion and spectral format shifts has shown that the most
accurate wavelength assignments (particularly in high dispersion) are obtained
when (a) the calibration images are taken close in time to the spectral image
to be extracted, (b) the spacecraft temperatures remain stable, and (c) the
calibration image and spectral image are of similar intensity. Although the
standard production processing includes a temperature and time correction
(amounting to a uniform shift) to a set of mean dispersion constants, there
has been evidence for occasional differential shifts in the spectral format
for which there is no correction or explanation. (The monitoring of the
biweekly wavelength calibration images showed that such an event occurred for
the LWR camera for several weeks in the fall of 1981). The possibility of
such occurrences would suggest that Guest Observers who require the most
accurate wavelength assignments should obtain their own calibration images and
request special processing. It should be pointed out, however, that (a)
fluctuating spacecraft temperatures will probably result in increased
wavelength errors with either of the calibration procedures, (b) errors due to
small-scale geometric distortions have been found to still exist with either
procedure, (c) variations in image intensity cannot be corrected for, and (d)
errors in centering the target in the aperture will still affect the
wavelength accuracy. This last caution is particularly pertinent in the case
of special calibrations since the cycling of the aperture mechanism required
to perform a wavelength calibration has been known to introduce shifts of
several pixels in the FES reference point used in target acquisition.
The special calibration procedure has become somewhat simplified in that
separate TFLOOD exposures are no longer necessary. Reseau positions can now
be directly measured from the WAVECAL images themselves (thereby eliminating
the need for the separate TFLOOD).
Some Guest Observers have found it useful to obtain WAVECAL images with their
normal spectral images and have them extracted using the standard production
processing procedure. The wavelength errors measured on the WAVECAL image can
then be used as a guide to correcting the other extracted spectral images.
Guest Observers who wish to use a special calibration should fill in the last
two lines of the "Processing Specifications" portion of the observing script
Section
(1)
indicating the image number of the special calibration to be
used. Guest Observers should also be warned that special processing requests
may cause some delay in the processing of their images.



![]()
![]()
![]()