


Next: 13 Assessing NEWSIPS Data
Up: 12 Final Archive Data
Previous: 12.8 Low-Dispersion Merged Extracted
The wavelengths, 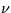 flags, and fluxes extracted from the SIHI are
stored in the MXHI as a binary table extension using fixed-length
floating point vectors. No primary data or additional extensions are
included.
flags, and fluxes extracted from the SIHI are
stored in the MXHI as a binary table extension using fixed-length
floating point vectors. No primary data or additional extensions are
included.
The binary table contains 17 fields of various data types. All vectors
are padded with zeroes (both before and after the extracted data) to
maintain a fixed length of 768 points. Wavelengths are uniformly sampled
for each order, are measured in vacuum, and have had the heliocentric
velocity correction applied. The width of each row (i.e.,
65 + 22 × 768 = 16961)
bytes, and the number of rows (i.e.,
NAXIS2) is equal to the number of extracted orders. In this
manner, all the information pertaining to one spectral order is
contained in one row of the binary table. The fields are defined in the
order shown below:
- Order number, one 8-bit byte.
- Number of extracted points n, one 16-bit integer.
- Starting wavelength, one double-precision floating point value.
- Starting pixel at starting wavelength, one 16-bit integer.
- Wavelength increment, one double-precision floating point value.
- Slit height in pixels, one single-precision floating point number.
- Line number for found centroid of spectrum, one single-precision
floating point number.
- Net flux spectrum, 768 single-precision floating point numbers
with n extracted data points.
- Background flux spectrum, 768 single-precision floating point
numbers with n extracted data points.
- Noise vector, 768 single-precision floating point numbers with
n extracted data points.
-
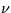 flags as n 16-bit integers stored in two's complement
form.
flags as n 16-bit integers stored in two's complement
form.
- Ripple-corrected net flux spectrum, 768 single-precision floating
with n extracted data points.
- Absolutely-calibrated, ripple-corrected net flux spectrum, 768
single-precision floating point numbers. with n extracted
data points.
- Start pixel for background fit, one 16-bit integer number.
*
- End pixel for background fit, one 16-bit integer number.
*
- Chebyshev scale factor, one single-precision floating point
number.
*
- Chebyshev polynomial coefficients for global background
correction, 7 single-precision floating point numbers.
*
Note that unlike the MXLO, SILO, and SIHI, the starting wavelengths
listed in the MXHI table do not refer to the first data point in the
flux vectors, but rather the starting pixel listed in field four. In
this manner, the 768-point flux vector can be mapped directly to the
768-pixel wide high-dispersion SI array.
As in low dispersion, since the absolute calibration covers the range of
1150-1980Å for short-wavelength spectra and 1850-3350Å for
long-wavelength spectra, data points outside this wavelength range are
set to 0 in the absolutely-calibrated flux vector. The net, background,
and noise vectors are not affected. (Note that unlike the sigma vector
in the MXLO file, the MXHI noise vector is uncalibrated.) Uncalibrated
data points are also flagged in the 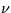 flag vector with a value of
-2. Table 12.11 shows the basic FITS Keywords for the MXHI.
flag vector with a value of
-2. Table 12.11 shows the basic FITS Keywords for the MXHI.
 IMPORTANT NOTE: Several adjustments must be made to the
last four parameters (fields 14-17) if the user wishes to evaluate the
Chebyshev coefficients in order to reproduce the background fluxes as
stored in the ninth field of the MXHI extension header. First, the
parameters have inadvertently been stored in the reverse order (i.e., the
parameters written in the first row of the table should have been stored
in the last row, the parameters for the second row in the second to last
row, etc.). So, for example, in the case of the LWR camera, the starting
and ending pixels, Chebyshev scale factor, and Chebyshev coefficients
found in row 1 (echelle order 127) actually pertain to row 61 (echelle
order 67). Second, the true starting pixel is 768 minus the stored
ending pixel and the true ending pixel is 768 minus the stored starting
pixel. These true pixel values must be used to correctly evaluate the
Chebyshev coefficients. Third, once the Chebyshev coefficients have been
evaluated, the resultant background ``fluxes'' must be scaled in the
following manner: multiply each background value by both the Chebyshev
scale factor and the corresponding extraction slit height then divide
this result by 32. Finally, the resultant array of background fluxes
which are produced upon evaluation of the Chebyshev coefficients must be
reversed (i.e., the computed background flux for pixel 1 becomes the
background flux for pixel 768 and vice versa). We emphasize that these
reversals and scalings are needed only when using the Chebyshev
parameters in fields 14-17 to reproduce the background fluxes-the
background fluxes themselves as contained in the ninth field are
correct.
IMPORTANT NOTE: Several adjustments must be made to the
last four parameters (fields 14-17) if the user wishes to evaluate the
Chebyshev coefficients in order to reproduce the background fluxes as
stored in the ninth field of the MXHI extension header. First, the
parameters have inadvertently been stored in the reverse order (i.e., the
parameters written in the first row of the table should have been stored
in the last row, the parameters for the second row in the second to last
row, etc.). So, for example, in the case of the LWR camera, the starting
and ending pixels, Chebyshev scale factor, and Chebyshev coefficients
found in row 1 (echelle order 127) actually pertain to row 61 (echelle
order 67). Second, the true starting pixel is 768 minus the stored
ending pixel and the true ending pixel is 768 minus the stored starting
pixel. These true pixel values must be used to correctly evaluate the
Chebyshev coefficients. Third, once the Chebyshev coefficients have been
evaluated, the resultant background ``fluxes'' must be scaled in the
following manner: multiply each background value by both the Chebyshev
scale factor and the corresponding extraction slit height then divide
this result by 32. Finally, the resultant array of background fluxes
which are produced upon evaluation of the Chebyshev coefficients must be
reversed (i.e., the computed background flux for pixel 1 becomes the
background flux for pixel 768 and vice versa). We emphasize that these
reversals and scalings are needed only when using the Chebyshev
parameters in fields 14-17 to reproduce the background fluxes-the
background fluxes themselves as contained in the ninth field are
correct.
Table 12.11:
MXHI - Basic FITS Keywords
| Keyword and value |
Description |
|---|
SIMPLE = T |
Standard FITS Format |
BITPIX = 8 |
Binary data |
NAXIS = 0 |
No image data |
EXTEND = T |
Extensions are present |
TELESCOP= 'IUE ' |
International Ultraviolet
Explorer |
DATE = 'dd/mm/yy' |
Date file was written |
ORIGIN = 'VILSPA ' |
Institution generating the file |
XTENSION= 'BINTABLE' |
Binary table extension |
BITPIX = 8 |
Binary data |
NAXIS = 2 |
Two-dimensional table array |
NAXIS1 = 16961 |
Width of row in bytes |
NAXIS2 = nn |
Number of orders |
PCOUNT = 0 |
Number of bytes following data matrix |
GCOUNT = 1 |
Only one group |
TFIELDS = 17 |
Number of columns in the table |
TFORM1 = '1B ' |
8-bit byte |
TTYPE1 = 'ORDER ' |
Order number |
TUNIT1 = ' ' |
Unitless |
TFORM2 = '1I ' |
16-bit integer |
TTYPE2 = 'NPOINTS ' |
Number of non-zero points |
TUNIT2 = ' ' |
Unitless |
TFORM3 = '1D ' |
Double precision |
TTYPE3 = 'WAVELENGTH' |
Starting wavelength |
TUNIT3 = 'ANGSTROM' |
Unit is Angstrom |
TFORM4 = '1I ' |
16-bit integer |
TTYPE4 = 'STARTPIX' |
Starting pixel at starting
wavelength |
TUNIT4 = 'PIXEL ' |
Unit is pixel |
TFORM5 = '1D ' |
Double precision value |
TTYPE5 = 'DELTAW ' |
Wavelength increment |
TUNIT5 = 'ANGSTROM' |
Unit is Angstrom |
TFORM6 = '1E ' |
Single precision |
TTYPE6 = 'SLIT HEIGHT' |
Height of extraction slit |
TUNIT6 = 'PIXEL ' |
Unit is pixel |
TFORM7 = '1E ' |
Single precision |
TTYPE7 = 'LINE_FOUND' |
Line number where spectral
centroid is found |
TUNIT7 = 'PIXEL ' |
Unit is pixel |
TFORM8 = '768E ' |
Single precision array |
TTYPE8 = 'NET ' |
Net flux array |
TUNIT8 = 'FN ' |
Unit is IUE Flux Number (FN) |
TFORM9 = '768E ' |
Single precision array |
TTYPE9 = 'BACKGROUND' |
Background flux array |
TUNIT9 = 'FN ' |
Unit is IUE Flux Number(FN) |
TFORM10 = '768E ' |
Single precision array |
TTYPE10 = 'NOISE ' |
Noise spectrum |
TUNIT10 = 'FN ' |
Unit is IUE Flux Number (FN) |
TFORM11 = '768I ' |
16-bit integer array |
TTYPE11 = 'QUALITY ' |
Data quality flag |
TUNIT11 = ' ' |
Unitless |
TFORM12 = '768E ' |
Single precision array |
TTYPE12 = 'RIPPLE ' |
Ripple-corrected net flux array |
TUNIT12 = 'FN ' |
Unit is IUE Flux Number (FN) |
TFORM13 = '768E ' |
Single precision array |
TTYPE13 = 'ABS_CAL ' |
Absolutely-calibrated net flux |
TUNIT13 = 'ERGS/CM2/S/A' |
Unit is ergs/cm2/sec/Angstrom |
TFORM14 = '1I ' |
16-bit integer |
TTYPE14 = 'START-BKG' |
Beginning pixel of background fit |
TUNIT14 = 'PIXEL ' |
X-axis in SIHI image |
TFORM15 = '1I ' |
16-bit integer |
TTYPE15 = 'END-BKG ' |
End pixel of background fit |
TUNIT15 = 'PIXEL ' |
X-axis in SIHI image |
TFORM16 = '1E ' |
Single precision |
TTYPE16 = 'SCALE_BKG' |
Chebychev scale factor |
TUNIT16 = ' ' |
Unitless |
TFORM17 = '7E ' |
Single precision array |
TTYPE17 = 'COEFF ' |
Chebychev coefficients of
background fit |
TUNIT17 = ' ' |
Unitless |
FILENAME= 'AAAnnnnn.MXHI' |
Filename (camera) (number) .MXHI |
EXTNAME = 'MEHI ' |
Name of table |



Next: 13 Assessing NEWSIPS Data
Up: 12 Final Archive Data
Previous: 12.8 Low-Dispersion Merged Extracted
Karen Levay
12/4/1997
![]() flags, and fluxes extracted from the SIHI are
stored in the MXHI as a binary table extension using fixed-length
floating point vectors. No primary data or additional extensions are
included.
flags, and fluxes extracted from the SIHI are
stored in the MXHI as a binary table extension using fixed-length
floating point vectors. No primary data or additional extensions are
included.
![]() flag vector with a value of
-2. Table 12.11 shows the basic FITS Keywords for the MXHI.
flag vector with a value of
-2. Table 12.11 shows the basic FITS Keywords for the MXHI.
![]() IMPORTANT NOTE: Several adjustments must be made to the
last four parameters (fields 14-17) if the user wishes to evaluate the
Chebyshev coefficients in order to reproduce the background fluxes as
stored in the ninth field of the MXHI extension header. First, the
parameters have inadvertently been stored in the reverse order (i.e., the
parameters written in the first row of the table should have been stored
in the last row, the parameters for the second row in the second to last
row, etc.). So, for example, in the case of the LWR camera, the starting
and ending pixels, Chebyshev scale factor, and Chebyshev coefficients
found in row 1 (echelle order 127) actually pertain to row 61 (echelle
order 67). Second, the true starting pixel is 768 minus the stored
ending pixel and the true ending pixel is 768 minus the stored starting
pixel. These true pixel values must be used to correctly evaluate the
Chebyshev coefficients. Third, once the Chebyshev coefficients have been
evaluated, the resultant background ``fluxes'' must be scaled in the
following manner: multiply each background value by both the Chebyshev
scale factor and the corresponding extraction slit height then divide
this result by 32. Finally, the resultant array of background fluxes
which are produced upon evaluation of the Chebyshev coefficients must be
reversed (i.e., the computed background flux for pixel 1 becomes the
background flux for pixel 768 and vice versa). We emphasize that these
reversals and scalings are needed only when using the Chebyshev
parameters in fields 14-17 to reproduce the background fluxes-the
background fluxes themselves as contained in the ninth field are
correct.
IMPORTANT NOTE: Several adjustments must be made to the
last four parameters (fields 14-17) if the user wishes to evaluate the
Chebyshev coefficients in order to reproduce the background fluxes as
stored in the ninth field of the MXHI extension header. First, the
parameters have inadvertently been stored in the reverse order (i.e., the
parameters written in the first row of the table should have been stored
in the last row, the parameters for the second row in the second to last
row, etc.). So, for example, in the case of the LWR camera, the starting
and ending pixels, Chebyshev scale factor, and Chebyshev coefficients
found in row 1 (echelle order 127) actually pertain to row 61 (echelle
order 67). Second, the true starting pixel is 768 minus the stored
ending pixel and the true ending pixel is 768 minus the stored starting
pixel. These true pixel values must be used to correctly evaluate the
Chebyshev coefficients. Third, once the Chebyshev coefficients have been
evaluated, the resultant background ``fluxes'' must be scaled in the
following manner: multiply each background value by both the Chebyshev
scale factor and the corresponding extraction slit height then divide
this result by 32. Finally, the resultant array of background fluxes
which are produced upon evaluation of the Chebyshev coefficients must be
reversed (i.e., the computed background flux for pixel 1 becomes the
background flux for pixel 768 and vice versa). We emphasize that these
reversals and scalings are needed only when using the Chebyshev
parameters in fields 14-17 to reproduce the background fluxes-the
background fluxes themselves as contained in the ninth field are
correct.