|
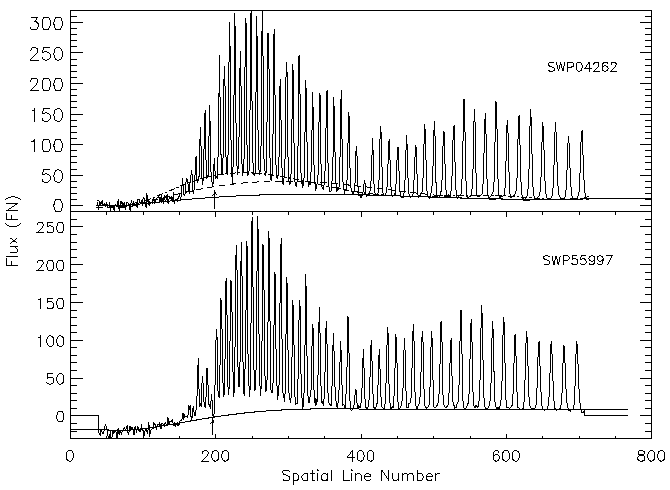
| Figure 7:
(Panel a): A comparison of the Pass 1 extraction
in the spatial direction with the Chebyshev solution for the early-epoch
image SWP04262. Three solutions are shown: the first, 7th-degree solution
before a pathology check (dashed line), the 5th-degree solution actually
accepted by the BCKGRD pipeline version (solid), and a ``customized"
solution obtained by the author using the IRAF task CONTINUUM by weighting
only the lower envelope of interorder fluxes (dot-dashed line). Note that none
of these solutions is a satisfactory fit to the true background level in all
regions. The location of Lyman (Panel b): A comparison of the Pass 1 extraction
in the spatial direction with the Chebyshev solution for the late-epoch image
SWP55997 of |
Next: Analysis of Null Images Up: Analysis of Scorpii Background Previous: Time Degradation of Background