



Next: Header
Up: FITS Fundamentals
Previous: IEEE Floating Point Data
The random groups structure (Greisen and Harten
1981) was originally designed for applications in radio astronomy but was intended
for other applications as well. It never gained acceptance outside the radio interferometry
community, and some FITS readers designed for other communities cannot read it.
In addition, the random groups records are a structural anomaly in FITS, as they
are the only records that do not conform to the primary HDU - extensions - special
records sequence. All of the original objectives originally intended for random
groups can now be achieved through the use of the now standard binary table format
described in section 3.6. Even the interferometry
community, for whom random groups was originally intended, is developing new conventions
based upon binary tables. Do not create FITS files using random groups; use binary
tables instead. The description of random groups presented here is intended as
a reference for those who may have to read old random groups FITS files, not as
an encouragement to write them. A number of keywords have been reserved for the
random groups structure, and may not be used for any other purpose, unless specifically
stated in the FITS rules. Also, the random groups structure is the original source
of the PCOUNT and GCOUNT keywords that were incorporated into
the Generalized Extensions rules discussed in section 3.3.
While the basic array structure of FITS can handle a data matrix when
the data are distributed evenly along all axes, sometimes the data may
not be distributed uniformly along one or more axes. The random
groups structure was created to handle such situations. Instead of being
followed by a data array, the primary header is followed by a special
set of records, of standard FITS 23040-bit size, called random groups
records. These records contain a series of groups, each consisting of a
sequence of parameters followed by an array. The parameters carry the
data whose spacing is not uniform and which are not ordered, i.e.,
random, hence the name. The number of random parameters and the
dimensions of the array must be the same in all groups.
On application is for uv interferometric visibility data;
in fact, random groups are
sometimes referred to as UV FITS. Consider a set of weighted complex
fringe visibilities for the four Stokes polarizations at a sequence of
evenly spaced frequencies. The axes are u, v, w, hour
angle, baseline, fringe visibility information (real part, complex part,
and weight), Stokes parameter, and frequency. The points along the
frequency axis are evenly spaced, and the fringe visibility and Stokes
axes can both be handled by using ``evenly spaced'' integer index points
to represent the separate components - real, complex, and weight - for the
visibility and the four Stokes parameters. Thus, an individual
observation can easily be structured as a matrix with axes of visibility
components, Stokes parameter, and frequency. However, the individual
matrices are at nonuniformly distributed values of baseline, hour angle,
and (u, v, w).
Using the random groups structure, the values of baseline, hour angle, and
(u, v, w) would be specified as parameters
before each (visibility, polarization, frequency) matrix. The combination of
parameters and array constitutes a group. The structure of the group would be
given by the form
| 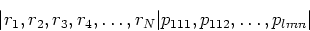 |
(3.6) |
corresponding, in this example, to
|u, v, w, time, baseline|(visibility
component, Stokes parameter, frequency)|
where 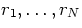 are random parameters 1 through N and
are random parameters 1 through N and
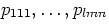 are pixel values in the order defined for
a data matrix. The value of p could, in principle, be as
large as 998 for each axis, as opposed to
the 999 maximum for Basic FITS.
The data array pijk starts immediately after the last
parameter, rN. The storage order and internal
representation of a random groups data array are the same as for a
Basic FITS simple array. It is interesting to note that the Basic FITS
data structure is actually a subset of this more general structure,
with no parameters.
are pixel values in the order defined for
a data matrix. The value of p could, in principle, be as
large as 998 for each axis, as opposed to
the 999 maximum for Basic FITS.
The data array pijk starts immediately after the last
parameter, rN. The storage order and internal
representation of a random groups data array are the same as for a
Basic FITS simple array. It is interesting to note that the Basic FITS
data structure is actually a subset of this more general structure,
with no parameters.




Next: Header Up: FITS Fundamentals Previous: IEEE Floating Point Data