




Next: C Implementation on Physical
Up: B Proposed Binary Table
Previous: B.2 ``Multidimensional Array'' Convention
This appendix
describes a layered convention for specifying that a
character array field (TFORMn = 'rA ') consists
of an array of either
fixed-length or variable-length substrings
within the field. This convention utilizes the option described in
the basic binary table definition to have additional characters
following the datatype code character in the TFORMn value
field. The full form for the value of TFORMn within this
convention is
'rA:SSTRw/nnn'
and a simpler form that may be used for fixed-length substrings only is
'rAw'
where
r is an integer giving the total length including any delimiters
(in characters) of the field,
A signifies that this is a character array field,
: indicates that a convention indicator follows,
SSTR indicates the use of the ``Substring Array'' convention,
w is an integer 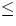 r giving the (maximum) number of
characters in an
individual substring (not including the delimiter), and
r giving the (maximum) number of
characters in an
individual substring (not including the delimiter), and
/nnn if present, indicates that the substrings
have variable-length and are delimited by an ASCII text character with
decimal value nnn in the range 032 to 126 decimal, inclusive.
This character is referred to as the delimiter character. The
delimiter character for the last substring will be an ASCII NUL.
To illustrate this usage:
'40A:SSTR8' signifies that the field is 40 characters wide and
consists of an array of 5 8-character fixed-length substrings. This
could also be expressed using the simpler form as '40A8'
'100A:SSTR8/032' signifies that the field is 100 characters wide
and consists of an array of variable-length substrings where each
substring has a maximum length of 8 characters and, except for the last
substring, is terminated by an ASCII SPACE (decimal 32) character.
Note that simple FITS readers that do not understand this
substring convention can ignore the TFORM characters
following the rA and can interpret the field
simply as a single long string
as described in the basic binary table definition.
The following rules complete the full definition of this convention:
- 1.
- In the case of fixed-length substrings, if r is not an
integer multiple of w then the remaining odd characters are
undefined and should be ignored. For example if
TFORMn ='14A:SSTR3', then the field contains 4
3-character substrings followed by 2 undefined characters.
- 2.
- Fixed-length substrings must always be padded with blanks if
they do not otherwise fill the fixed-length subfield. The ASCII NUL
character must not be used to terminate a fixed-length substring
field.
- 3.
- The character following the delimiter character in
variable-length substrings is the first character of the following
substring.
- 4.
- The method of signifying an undefined or null substring within a
fixed-length substring array is not explicitly defined by this
convention (note that there is no ambiguity if the variable-length
format is used). In most cases it is recommended that a completely
blank substring or other adopted convention (e.g.
'INDEF') be
used for this purpose although general readers are not expected to
recognize these as undefined strings. In cases where it is necessary
to make a distinction between a blank, or other, substring and an
undefined substring use of variable-length substrings is recommended.
- 5.
- Undefined or null variable-length substrings are designated by a
zero-length substring, i.e., by a delimiter character (or an ASCII NUL
if it is the last substring in the table field) in the first position
of the substring. An ASCII NUL in the first character of the table
field indicates that the field contains no defined variable-length
substrings.
- 6.
- The ``Multidimensional Array''convention described in
Appendix B.2 of this paper provides a syntax using the
TDIMn keyword
for describing multidimensional arrays of any
datatype which can also be used to represent arrays of fixed-length
substrings. For a one dimensional array of substrings (a two
dimensional array of characters) the ``Substring Array'' convention is
preferred over the ``Multidimensional Array'' convention.
Multidimensional arrays of (fixed length) strings require the use of
the ``Multidimensional Array'' convention.
- 7.
- This substring convention may be used in conjunction with
the ``Variable Length Array'' facility described in
Appendix B.1 of this paper. In this case, the two
possible full forms for the value of the TFORM keyword are
TFORMn = 'rPA(emax):SSTRw/nnn'
and
TFORMn = 'rPA(emax):SSTRw'
for the variable and fixed cases, respectively.
This convention is optional and will not preclude other conventions.
This convention is not part of the binary table definition.





Next: C Implementation on Physical
Up: B Proposed Binary Table
Previous: B.2 ``Multidimensional Array'' Convention
5/13/1999
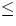 r giving the (maximum) number of
characters in an
individual substring (not including the delimiter), and
r giving the (maximum) number of
characters in an
individual substring (not including the delimiter), and